Unsolve
by Aidan Glickman
Published: 2023-06-01T08:00:00-0400
"The process of assessing how you feel about the things you own, identifying those that have fulfilled their purpose, expressing your gratitude, and bidding them farewell, is really about examining your inner self, a rite of passage to a new life." - Marie Kondo
Too often in life, we choose to hold onto things simply because they are there, when in truth we no longer need them. Since I recently graduated and am moving to a new city, I've been thinking a lot about what things actually matter.
- "Will I really wear that old pair of shoes?" (probably not)
- "Do I need a backup to my backup soldering iron?" (without a doubt)
- "Is the seven in spot r2c3 really necessary?" (hmm...1)
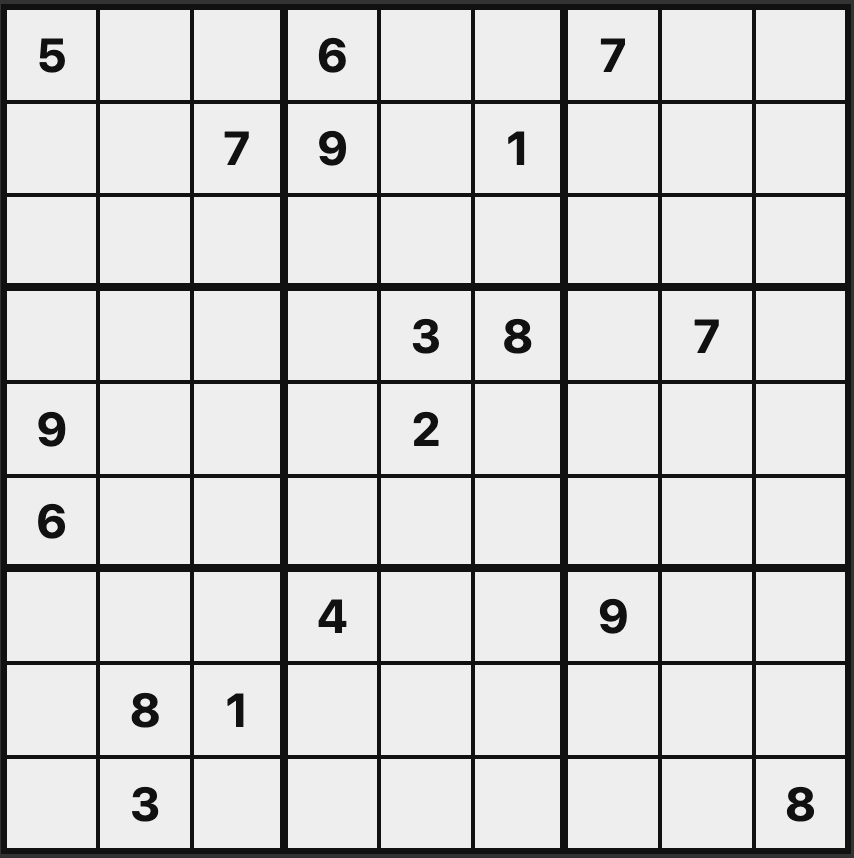
And while Ms. Kondo may have wavered in her dedication to tidying2, I don't think that is any reason not to apply her teachings to logic puzzles. In an effort to do just that, we introduce unsolve, a game which taxes you with trying to "tidy up" a sudoku as much as possible while keeping the solution unique.
The Mathematics of Sudoku3
When Sudoku rose to global popularity in the early 2000s, there was a (relatively shortlived) pop-science obsession with some of the mathematical features of the Japanese game. The two most researched questions in the field were "How many filled Sudoku grids are there?4" and "What is the lowest number of clues necessary to form a valid puzzle?5"6. While these questions are interesting big picture takes on the game, they don't give us too much insight on patterns in individual puzzles.
To remedy this, we present the question "what is the smallest minimal form of a given Sudoku?" That is, what is the smallest number of clues for a given grid that result in a unique solution? If we can find such a solution for any given puzzle, we can actually automate the generation of relatively hard puzzles, since writing out filled grids is already pretty easy.
The (General) Solution
While everything that we have discussed so far applies only to Sudoku, we wanted our solution to generalize a bit more than that. In fact, the backend of Unsolve can easily be extended to work for any game that can be modeled as a constraint satisfaction problem in Z37.
Any puzzle can be coded using two separate groups of constraints; One set encodes the rules of the game8, and one that encodes the restrictions that make up the actual puzzle9. When it comes to trying to minimize a puzzle, we really just want to remove as many constraints from the second set while keeping the solution unique.
To accomplish this in the general case, there really is no option except to do a massive brute force search10. This is obviously not feasible for lots of types of games, since there can be a huge number of possible sets of clues11, so, what do we do?
The (Unsolve) Solution
For the purposes of this project, we put general games on the back-burner, and switched our focus to Sudoku specifically. While we have determined that globally minimizing Sudoku puzzles is rather difficult, finding an arbitrary number of local minima is not very hard. One such strategy to do this could be to pick 17 random clues to fix (since we know there are no unique puzzles with fewer) and incrementally add clues until we get to a unique puzzle.
Unavoidable Sets
We can combine this strategy with an interesting feature of Sudoku puzzles, namely the existence of unavoidable sets. Unavoidable sets are sets of cells within a puzzle where at least one of the cell values must be given for a puzzle to be unique.
Consider this example from Sudopedia:
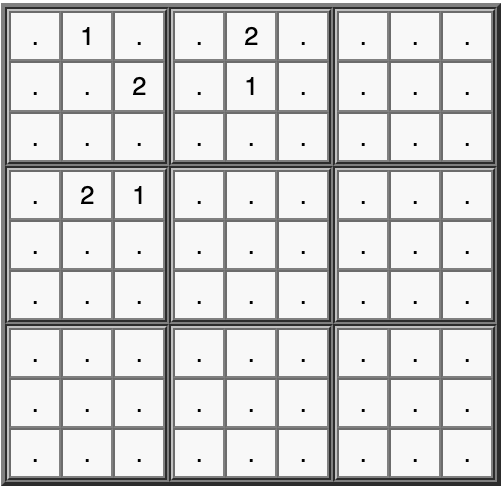
If none of the six given cells were filled, then the puzzle could not be unique, since all of the ones and twos could be swapped, yielding another viable solution.
There are many different patterns of unavoidable sets, and enumerating some of these sets was a crucial strategy used in the paper that confirmed that there are no 16 clue Sudokus12. By using members of these unavoidable sets as members of our initial random sets, we have a higher probability of finding viable solutions with fewer clues, since we know that at least one of these clues must be included. This strategy made up the original puzzle set used for Unsolve, and can easily be used to generate pretty good™️ Sudokus.
The Game
Now that we have set up just how hard this task is (even for a computer!) Why not jump right in and try your hand at it? My friends Adam Aaronson13 and Aakash Narayan14 and I, under the supervision of Professor Ben Cosman turned this ridiculous task into a little web toy. Simply put in a seed (any number will do), hit generate puzzle, and tidy away! The game ends when your solution is no longer unique.
The Reveal Button
One inclusion that may seem interesting based on the computational challenges listed above, is the reveal button which we guarantee always provides a perfectly optimal solution to a given problem. How did we accomplish this task? By cheating, of course! Since minimizing Sudokus is hard but solving them is easy, we simply used a list of known 17-clue puzzles, solve them in bulk to generate our starting puzzles, then randomly permute the symbols to make them look more unique15.
Player Strategy
While you might expect to see some tips on optimal play, unfortunately that would be impossible (see all of the computational challenges outlined above). Instead, all I can offer is one key observation that stems from forcing my friends and family to play.
Players tend to be really drawn to making quick progress at the expense of long term success16, leading to attractive-seeming but destructive strategies like removing every instance of a specific number, or knocking out an entire row, column or box. This strategy is not inherently wrong (see the example below which contains no ones and has the third row knocked out) but it does drastically cut down your options down the line17.
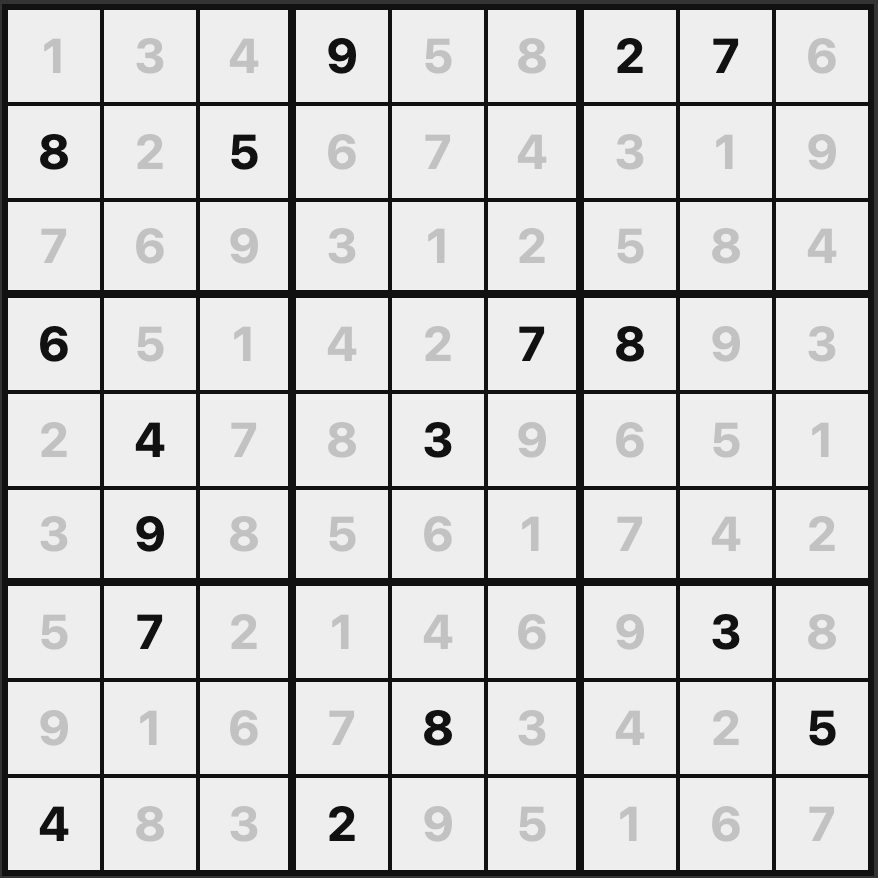
The core strategy is really to try to find small(-ish) unavoidable sets, and allow the decision of which elements of those sets you keep to guide the decisions of what other clues you keep18.
Conclusion
I hope you had fun learning about some of the math behind Sudoku and puzzle setting, and that you will join me in wasting a few hours trying to figure out anything at all about this game. Unsolve is available here, and our source code is available here. This project was built as part of a CS 497 Team Project at UIUC in Spring of 2023.
Footnotes
-
No, the puzzle is actually in its minimal form if you remove that clue, but we'll get into that a bit more later. ↩
-
6,670,903,752,021,072,936,960 as counted in Mathematics of Sudoku I (Felgenhauser, Jarvis), although there are only 5,472,730,538 "essentially different" grids, when you consider transformations like rotation, relabeling clues, etc. (Mathematics of Sudoku II (Russell, Jarvis)) ↩
-
For a Sudoku to be considered "valid" it must have only one solution. We call it "minimal" if removing a clue would make it invalid. ↩
-
The answer to this question was eventually found to be 17, not through any crazy mathematical insight, but by literally enumerating every 16 clue puzzle with some shortcuts (https://www.math.ie/McGuire_V2.pdf) ↩
-
In the case of sudoku this would be the uniqueness within rows, columns and boxes ↩
-
The numbers that are given in certain boxes ↩
-
That is, to exhaustively search every single set of constraints to remove ↩
-
For any specific Sudoku, we can quickly count the number of clue sets by considering the local choice of whether or not to include each clue, for a staggering 2^81 = 2,417,851,639,229,258,349,412,352 clue sets, clearly not searchable in a reasonable time ↩
-
The aforementioned McGuire paper explains this strategy well, but I find it more entertaining to explore the sheer horror that is the inline x86 assembly used in the source code ↩
-
Frontend guru ↩
-
Sudoku puzzle generation specialist ↩
-
This is just one of the translations that are valid to perform on sudoku puzzles, other include transposing the puzzle, permuting rows or columns within a block, or permuting blocks row or column wise ↩
-
Yet another logic puzzle insight applicable to life as a whole ↩
-
To understand why, consider all of the translations that are valid while keeping a sudoku essentially equivalent. If you remove all of the ones from a puzzle, you certainly cannot remove all of another number (since you could then switch the two). This concept is closely related to that of unavoidable sets ↩
-
Yes, this advice is extremely vague and difficult to act on. I have yet to find an actual human who is "good" at this game. If you are please let me know! ↩